
What is a negative number? This is a hard enough question in its own right, but it’s closely related to another really tough question.
That other question is one that confuses and frustrates so many students in Middle School math, not to mention most adults. Here it is:
What does subtracting a negative number mean?
In order to answer that question, we need to clear up some common misconceptions about subtracting in general, and what a negative number is.
In earlier papers, I pointed out some things that are needed in order to answer this question.
In one, I defined subtraction as finding the missing addend in an addition statement. In another, I illustrated how this can be represented on a number line.
Here, I’ll take a look at the third issue above: What is a negative number? So, just what is a negative number? Doesn’t everyone know?
If you asked 100 high school graduates at random, at least 99 of them would probably say that a negative number is a number that is “less than zero” (if, of course, they know anything about math.)
But what does that really “mean.”
Perhaps surprisingly, this was a mystery to even the best mathematicians long after they resolved much tougher issues in math.
It wasn’t until the middle of the 1500s that mathematicians finally starting accepting negative numbers as “real’ (as in, not fake) numbers, and the process didn’t get completed until the 1800s.
Here’s the critical issue that made them so hard to accept, even at that late date. The following is a paraphrase of a question posed by De Morgan, a distinguished English Mathematician, in the 1800s:
How can you have negative 5 apples
(or any other object you can think of)?
That’s a pretty weird idea, isn’t it?

Well, it turns out you can’t have a negative number of apples. (But that will have to wait for later for more detail.)
A big breakthrough in thinking on this issue was actually related to the use of the number line to represent numbers. Many people feel that John Wallis, and English mathematician, was the first to use a pictorial diagram of number line in the late 1600s.
Using a number line, he represented positive numbers as numbers to the right of zero, and negative numbers as numbers to the left of zero like this:
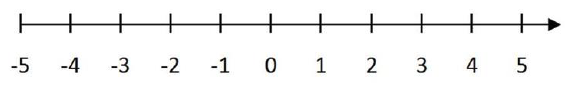
This representation later helped to resolve a lot of the anxiety over negative numbers.
And, of course, when you show negative numbers on a number line like this, and you count them from zero, a negative number does indeed, lie to the left of zero.

The problem is, that’s not what a negative number “really is.” In other words, that’s not the real definition of a negative number.
One reason this is the case is that you don’t have to count numbers starting at 0. Numbers can be counted by starting at any point on a number line. (Otherwise you couldn’t show adding or subtracting on a number line, among other things.)
This is a fundamental point that is almost never made in teaching math in elementary school. But it’s critical.
Here’s why.
Mathematicians don’t actually define what a “negative number” is directly. They define a negative number in terms of the “additive inverse” of a number.
An additive inverse of a number, X, is defined as the number you add to X to get zero. Here’s what that looks like on a number line.
Let’s say that X is 5, so we put 5 on the number line.

In order to add a number to 5, we start counting at 5 for the second number.

Where we have to end up, according to the definition of an additive inverse, is 0.
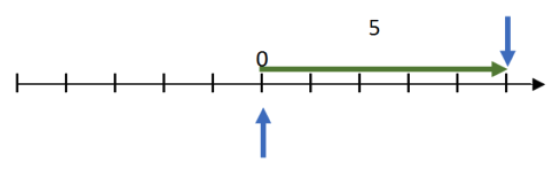
If we start counting at 5 and we want to end up at 0, which direction do we have to count?
We have to count to the left. When we do that, it looks like this.
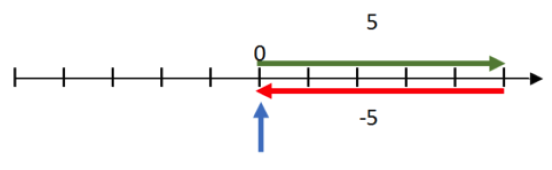
The number shown in red is negative 5…by definition.
Does -5 lie to the left of zero?
No, not in this case.
Is it really a negative number?
Yes. That’s how a negative number is defined. A negative number is the inverse of a positive number.
And what is the inverse of 5?
It’s the number you need to add when you start counting at 5 and want to end up at 0. But now let’s look at a different situation.
Let’s say we wanted to add the inverse of 5, which we now know is -5, to 0, instead of to 5. What would that look like?
We start counting at 0…
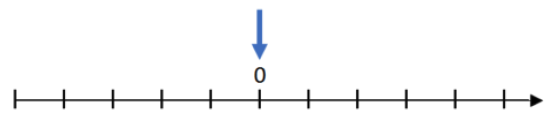
…and we count the inverse of 5, which is -5.
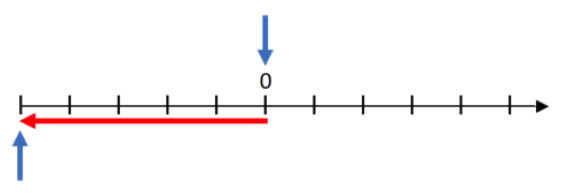
The point where we end up represents -5. The red arrow shows negative 5 below.

Note that -5, the red arrow pointing to the left, is exactly the same number as -5 in the example above, which is also the red arrow pointing to the left.
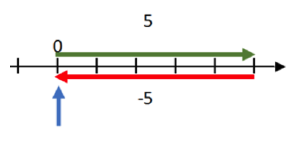
The fact that the two red arrows start at different locations on the number line, and end up at different locations, doesn’t affect what the number is.
In each case, you count the same number of units. The only difference is where you start counting.
Of course, the other important point is the direction you count in. In each case, the 5 units are counted to the left.
That’s why it’s a negative number.
So, in order to name a negative number, we need to know two things:
And it doesn’t matter where you start counting.
So here’s the difference in a positive number and a negative number:
That’s it.
This is also why we describe a negative number as the “opposite” of a positive number. It’s counted in the opposite direction.
The actual direction each kind of number is counted is not important in an absolute sense. We could have decided, as a culture, to count positive numbers to the left and negative numbers to the right. it’s just a historical accident that we count positive numbers to the right.
Once counting positive numbers to the right was accepted, the “opposite” became counting to the left. The real distinction is that the directions are different.
And, finally, of course, negative numbers still do “lie to the left of 0”, but only when we count them starting at 0, which is not a requirement of a negative number, or a positive number for that matter.
See others in this series:
Click below for other Resources