
I would argue that in teaching math in America, we don’t take full advantage of the critical concept of place value.
One important implication is the fact that:
American kids take 3 years or more to become fluent with basic math facts (if they ever do)…
while kids the same age in East Asian countries are fluent by the end of first grade.
So, you ask, what does place value have to do with learning the basic math facts and becoming fluent with them?
As it turns out…plenty.
In the U.S., we teach the addition and subtraction facts using the digits 1-9 in all possible combinations, which results in 81 total facts.
For over 100 years, American education researchers have documented the fact that 36 of these, the facts with sums up to 10, are the easiest. Another 36, the facts with sums over 10, are much more difficult. The remaining 9 facts that sum to 10 are between these other two groups in difficulty.
For subtraction, you have the same number of facts since the “sum” for addition becomes the “minuend” for subtraction. (The minuend in subtraction is the number you subtract from. For more information, see the paper “What is Subtraction”)
The most difficult facts (with sums or minuends over 10, such as 8+7) often take years for students to remember and become fluent with. Many never become fluent with these facts. The biggest difference in the performance of American and East Asian students in first grade occurs for these harder facts.
Here’s why.
In America, we treat all the facts the same when having students learn them.
In other words, we too frequently have students practice all 81 of them over and over until they eventually remember them. Like me, you too may have learned by rote practice using flash cards.
This might be surprising, but in East Asian countries that’s not how they teach the facts with sums or minuends over 10. That’s the main reason they learn them faster.
The approach they use is called the “tens complement” approach. (In this country it’s often referred to as the “make a ten” approach.)
The term “tens complement” approach comes from the fact that it’s based on using “complements of ten,” pairs of numbers that add to ten, like 9 + 1, 7 + 3, and 6 + 4. At iLearn, we call these pairs of numbers that add up to 10 “TenPals™.”
I advocate this approach because it is widely documented as effective in East Asian countries, and has been documented by research to be very effective in this country as well. In fact, studies have been conducted as far back as the 1930s that document its effectiveness.
When you add two numbers with a sum over ten, like 9 + 6, for example, you are actually using place value, whether you realize it or not.
More recently, Fuson and her associates (e.g., Fuson, 1992; Fuson and Kwon, 1992) have done extensive research on this approach, both in the U.S. and Asia.
What the “tens complement,” or “TenPals™,” approach means is this.
When you add two numbers with a sum over ten, like 9 + 6, for example, you are actually using place value, whether you realize it or not. The vast majority of students in the U.S. never realize this because it’s not pointed out (i.e., it’s not made explicit), and historically, it hasn’t been part of learning these basic facts.
But, when you do teach these facts by explicitly teaching the role of place value, the process of memorizing the facts becomes dramatically easier.
Unfortunately, many adults who hear of this for the first time are resistant to this approach. That’s understandable given the fact that virtually all of them have learned facts without any regard to place value.
That includes me. I learned the basic facts by memorizing them the way everyone else did. When I first encountered the tens complement approach (courtesy of an employee of mine from South Korea) about 20 years ago, I was skeptical too. And it took me a while to “get it” and really understand the approach.
And, what’s truly remarkable is how much easier it is for these kids to memorize the facts using this approach.
So, let’s look at how this approach works and why it’s beneficial.
The tens complement (TenPals™) approach is based on the fact that students have previously mastered three groups of facts:
These must be learned in advance because they must be used in applying the tens complement (TenPals™) approach, with both addition and subtraction.
Let’s start with addition, for example, 9 + 5. Here’s an illustration. We start with 9.
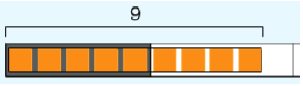
Then we add 5.
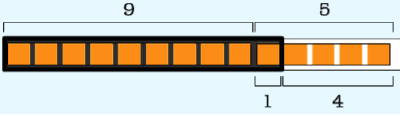
From previously mastered group 2 above, students already know that 9 + 1 = 10, so the first step is to “make a ten,” as illustrated by the bottom bracket above.
To do this, you use the tens complement of 9, which is 1. You subtract 1 from 5, add the 1 to the 9 to make 10.
Subtracting 1 from 5, leaves 4. (Because of prerequisite 1 above, we know that 5 – 1 = 4.) This is illustrated by the bracket below the 4 above.
Next you add the 4 to the 10 made earlier, to get 14. Because of previously mastered group 3 above, we know that 10 + 4 = 14.
So 9 + 5 is the same as 10 + 4, which equals 14. So 9 + 5 = 14.
This may sound complicated, but it’s really not. These are the mathematical steps behind the process. The teaching process relies more on animated visual representations like the one above than written representations, and it’s much easier to understand.
Since the advent of the Common Core State Standards in math, some have posted criticisms of this approach in social media.
“It’s too complicated”
As just noted, one criticism is: it’s way too complicated. Why not just “memorize” these facts, not use some “complicated” rule to learn them.
This criticism would be valid if you only had to learn this one fact. Learning it that way would be a huge waste of time.
But here’s the problem - kids don’t just have one difficult fact to learn. They have 36 of them to learn, and these are just for addition. There are 36 more for subtraction.
That’s a game changer that makes this argument irrelevant, as I’ll get into more below.
The second major criticism comes from the fact that after one has already learned these facts, as most adults criticizing this approach have, it’s virtually impossible to see the benefits of a different strategy.
The reality, is, however, as I noted above, that when you’re learning the facts for the first time it IS EASIER to learn using this approach than just memorizing. That’s what research in this country has shown.
It’s too slow
But you may still be thinking: Doesn’t this slow down learning when you have to apply this seemingly complicated rule?
No. It actually speeds up learning. And, that’s a powerful benefit - benefit number one.
Benefit #1:
Learning the basic facts using the TenPals™ approach takes much less time than it would by trying to remember these 36 difficult addition and 36 subtraction facts by repetition alone.
Why?
It results in a huge reduction in the number of things that have to be learned. Learning one strategy that easily generalizes to 36 different facts (actually 36 addition and 36 subtraction) is almost like learning one thing instead of 36.
It doesn’t speed things up quite that much, but the improvement is still dramatic.
The individual steps in applying the strategy are all easy for the child because they’ve already learned the prerequisites.
So, in addition to these prerequisite facts, the ONLY thing the child has to learn for all these addition facts is a single “rule.” This one rule applies to ALL addition facts with sums over 10 - that is, all the difficult facts. (This “rule” is actually a general principle that is conceptually grounded, not an arbitrary rule to be memorized, which we’ll come back to later.) The same is true for subtraction – one rule allows you to solve all 36 of the difficult subtraction facts.
By learning only one rule, you can accurately answer EVERY difficult fact, with a sum or minuend over 10, in short order.
And it’s only when a high level of accuracy has been reached that additional practice leads to fluency (because real fluency requires high levels of accuracy as well.)
But how does it ever produce fluency when you have to think through these steps?
Well for starters, developing accuracy is the first step in becoming fluent. Using this strategy makes it much easier to first develop accuracy with the facts. That’s benefit number two.
Benefit #2:
Practice is great for remembering what you’ve already learned, but it’s not that great for learning something the first time. Because of that, when you memorize the facts by sheer repetition, you first have to learn to recall the facts accurately…and you make a lot of errors.
The use of the TenPals™ strategy dramatically reduces the rate of errors while learning, which makes it far easier to answer accurately.
So when you practice, you’re practicing correct answers, not errors.
Here’s an example.
A mom asks her child: ”What’s 8 + 7?”
The first time the child hears this, she has no clue how to answer. She hasn’t “learned it.”
So here are the choices, Mom can keep asking her daughter to answer a set of different facts until eventually she hears 8 + 7 = 15 often enough that she can recall “15.” But this typically involves a long time and a lot of errors along the way.
And quite often, this results in a lot of frustration that makes it hard to continue trying…followed by a lot of resistance and avoidance.
With the TenPals™ strategy, the answer to all the hard addition facts can be derived from the one rule needed for all the facts.
For example, 8 + 7 is the same thing as 8 + 2 + 5, which is 15. So, if she knows the rule, she can find the answer easily.
This basically eliminates the trial and error process of learning the facts initially.
But what about fluency?
Benefit #3:
Building fluency is perhaps the biggest benefit.
This benefit is one that’s based purely on scientific research. Research has proven that as you repeat the process, you rely on the conscious thought process less and less. It’s something that just happens naturally with practice. You start “remembering” the answer without even thinking about it.
In other words, thinking about it consciously leads to the point where you no longer have to think about it to get to the end result. It may sound paradoxical, but it’s proven by research to be true.
And it feels almost magical, because you aren’t even aware it’s happening.
And here’s one last, huge additional benefit, benefit number four.
Benefit #4:
When students learn the facts this way, they almost never count on their fingers. Finger counting has been shown to be the biggest roadblock in memorizing the facts. Once kids start relying on finger counting to add and subtract, they often never stop using this approach and fail to transition to true “recall” from memory.
So what does all of this have to do with place value?
Well…that’s actually a trick question.
What I have referred to above as the “rule” for deriving the facts using the TenPals™ approach is not an arbitrary rule. It’s actually an application of the basic principle of place value.
In order to “make a ten” you learn that “making a ten” is the essence of place value. For sums greater than 9, you can’t write the sum with a single digit. It takes two digits, which means you have to write the sum using two “places” - the “ones” place and the “tens” place.
Any number greater than 9 cannot be written with one digit. You must use two digits, and when you use the second digit, you are using place value. The “1” in “10” does not actually mean “1.” It means “one unit more than “9” which we write as “10.” Because the “1” is written in the “second place,” or the “tens place” of the number, it means something different – it means ten ones, not one.
As students learn to apply this principle explicitly, they come to see that in order to write any 2-digit number, they must “make a ten” in the process. And the resulting number always has two digits.
So, when students learn to construct sums over ten in this manner, they are explicitly learning to apply the critical principal of place value.
In the traditional approach to teaching place value in America, this basic principle of place value is not introduced until later, when students are taught to add 2, two-digit numbers (like 18+14). That’s the first time they learn about “carrying a 1” or “regrouping.”
The problem with the traditional approach is the frequent criticism that students don’t understand what “carrying” or “regrouping” means. That should be expected, since it often comes across as just an arbitrary rule related to adding bigger numbers, which is not the case.
By learning this principle explicitly with the basic facts with sums from 11 through 19, students are better able to understand how it’s used when they learn to add two, 2-digit numbers. They see it as the same thing they did to “make a ten,” a ten being the simplest 2-digit number. (Of course, we don’t refer to this as a “principle,” they just understand it as part of how math works.)
This puts students far ahead of the game as it is currently pursued in American math education.
To me this is a very important issue that has huge potential benefits. Failure to recognize the value of this approach is why Americans so quickly start to lag far behind students in other countries – particularly East Asian countries like China, Japan, South Korea and Singapore.
There is one final oddity about learning the basic facts that is related to the TenPals™ strategy. Many advocates of “reform” math have for years advocated the use of “doubles” and “near-doubles” as strategies to use in learning the basic facts. See the post “Learning the Basic Facts – Doubles vs. Tens Complements“ for a comparison of the “doubles strategy” to the use of “TenPalsTM” in learning the basic addition and subtraction facts, along with multiple reasons why the tens complement, or TenPals™ approach is far superior.
Click below for other Resources